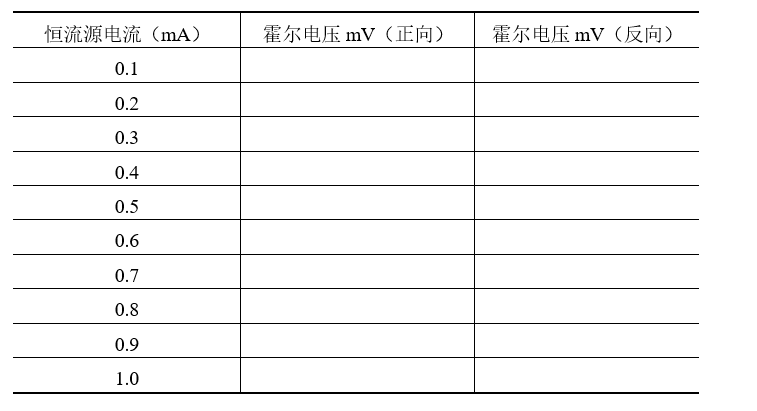
如图3-1所示，一矩形半导体薄片，当沿其x方向通有均匀电流I，沿Z方向加有均匀磁感应强度的磁场时，则在y方向上产生电势差。这种现象叫霍尔效应。

所生电势差用V_H表示，成为霍尔电压，其相应的电场称为霍尔电场Ey。实验表明，在弱磁场下，Ey同J（电流密度）和B成正比

                                                                                                             （1）

式中R_H为比例系数，称为霍尔系数。

在不同的温度范围，RH有不同的表达式。在本征电离完全可以忽略的杂质电离区，且主要只有一种载流子的情况，当不考虑载流子速度的统计分布时，对空穴浓度为p的P型样品

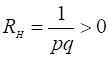                                                                                                            （2）

式中q为电子电量。对电子浓度为n的N型样品

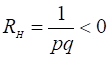                                                                                                            （3）

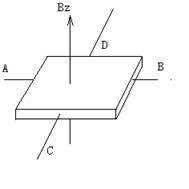
图3-1

当考虑载流子速度的统计分布时，式（2）、（3）应分别修改为

                                                                         （4）

式中μH为霍尔迁移率。μ为电导迁移率。对于简单能带结构

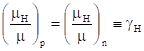                                                                                                         （5）

g_H称为霍尔因子，其值与半导体内的散射机制有关，对晶格散射g_H=3p/8=1.18;对电离杂质散射g_H=315p/512=1.93,在一般粗略计算中,g_H可近似取为1.

在半导体中主要由一种载流子导电的情况下，电导率为

                                                        和                                               （6）

由式（4）得到

                                                      和                                         （7）

测得R_H和σ后，μ_H为已知，再由μ（N，T）实验曲线用逐步逼近法查得μ，即可由式（4）算得n或p。这样得到的γh=μH/μ，已计入了多种散射同时存在的影响和能带结构修正。

在温度较高时,半导体进入过渡区和本征导电范围,必须考虑样品中同时存在两种载流子的影响.在弱电场条件下,可以证明

                                                                                                         (8)

式中b=μn/μp。对N型半导体

                                                               n=ND-NA+p                                                      （9）

对P型半导体

                                                               p=NA-ND+n                                                      （10）

如只考虑晶格散射，电导率为

                                                                                                           （11）

式中μLn和μLp和分别为电子的晶格散射迁移率，这里b=μLn/μLp。由式（9）、（10）和（11）可得

                                                      N型                                           （12）

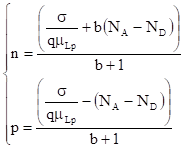                                                      P型                                           （13）

μLn和μLp可查阅实验手册。当b已知，便可由测得的电导率计算出n和p的值。

步骤（1）对于电磁铁的磁化电流I_M为定值（相应有一个确定的磁场B，参见仪器上标签），取10种不同的工作电流I_S（0~10mA），测量相应的霍尔电压V_H，共测量5个工作点（Bi，i=1，2，3，4，5），具体如下：

步骤（2）对于每个B_i，横坐标取工作电流IS，纵坐标取霍尔电压VH，理论上得到一条通过坐标原点“0”的倾斜直线，计算其斜率RHB／d，求其平均值

；根据己知的B和d（0.2mm），求得其霍尔系数RHi。

步骤（3）计算五个工作点的霍尔系数平均值。

步骤（4）根据和己知载流子的电量e，可求得载流子浓度n。