特性粘数[η]与分子量的关系

实验证明，当聚合物、溶剂和温度确定以后，[η]的数值仅由试样的分子量 M 决定，即

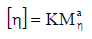
这 是 一 个 分 子 量 实 际 测 定 中 习 用 的 、 含 有 两 个 参 数 的 经 验 公 式 ， 称 之 为 Mark-Houwink 非线性方程。这样，只要知道参数 K 和α值，即可根据所测的[η]值计算 试样的粘均分子量 M 。

K 值与体系性质有关，但关系不大，仅随聚合物分子量的增大而有些减小(在一定的 分子量范围内可视为常数)，随温度增加而略有下降；而α值却反映高分子在溶液中的形 态，取决于温度、高分子和溶剂的性质。α一般在 0.5-1 之间。线型柔性链大分子在良溶 剂中，线团松懈，α接近于 0.8。溶剂溶解能力减弱，α值逐渐减小。在θ溶剂中，高分 于线团紧缩，α为 0.5。对于硬棒状的刚性高分子链α→2。其次，温度升高，有利于高 分子线团的松懈。在良溶剂中，线团本身已很松懈，因此温度上升对α的影响不大。在 不良溶剂中，线团端曲，温度升高使聚合物的内聚力减小，高分子线团松懈，α值增大。 最后，对于同一高分子—溶剂体系，高分子链越长，它在溶液中弯曲、缠结趋向越大， 所以分子量范围不同时，α值不同，只是在一定的分子量范围内，α值可视为常数。总之，对于一定的高分子—溶剂体系，在一定的温度下，一定的分子量范围内，K 和α值 为常数。用粘度法测得的分子量为粘均分子量。

参数 K 和α的测定方法

在[η]-M 方程中，参数 K 和α的测定方法如下。

首先，将聚合物试样进行分级，以获得分子量从小到大且分子量比较均一的级分。然后采用其他方法测定各级分的平均分子量，并测定特性粘度。

因为

以[η]对 lgM 作图，其斜率即为α，截距即为 lgK。表 4-2 列出 了某些聚合物-溶剂体系的 K 和α值。

高分子溶液粘度测定

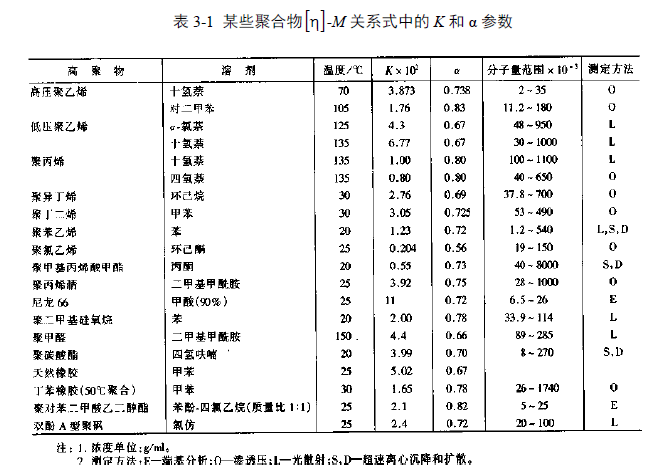
测定高分子溶液粘度时，以毛细管粘度计最为方便。 常用的毛细管粘度计由三支管组成，称为 Ubbelobde 型，简称乌氏粘度计，如图 3-1 所示。粘度计具有一根内径为 R、长度为l 的毛 细管，毛细管上端有一个体积为 V 的小球，小球上下有刻线α和 b。待测液体自 A 管加入，经 B 管将其吸至 a 线以上，再使 B 管通大气， 图 3-1 乌氏粘度计 任其自然流下，记录液面流经 a 及 b 线的时间 t。这样，外加的力就是高度为 h 的液体自 身的重力 P。

假定液体流动时没有湍流发生，即外加力 P 全部用以克服液体对流动的粘滞阻力， 则可将牛顿粘性流动定律应用于液体在毛细管中的流动．得到泊松义耳(Poiseuille)定律，又称 R⁴ 定律。

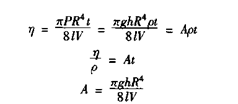
式中η/ ρ ——比密粘度，单位 Stokes； A——仪器常数。

实验时，在恒定条件下，用同一支粘度计测定几种不同浓度的溶液和纯溶剂的流出 时间 t 及 t₀，由于极稀溶液中溶液和溶剂的密度近似相等， ρ≈ρ₀ ，所以

这样，由纯溶剂的流出时间 t₀ 和溶液的流出时间t 即可求出溶液的相对粘度η_r 。

 一般，选用合适的粘度计使待测溶液和溶剂的流出时间大于 100s，则能满足没有湍流的假定。

如果流速较大，外加力除了用以驱动液体流动以外，同时也使液体得到了动能．这 部分能量的消耗须予以改正，称为动能改正。

求出了相对粘度之后，根据粘度对浓度的依赖关系

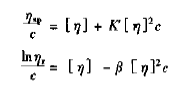
只要配制几个不同浓度的溶液，分别测定溶液及纯溶剂的粘度，然后计算出η_sp /c ，lnη_r /c 在同一张图上作对η_sp /c 、lnη_r /c对 c 的图，两条直线外推至 c→0，其共同的 截距即为[η]。

以上浓度外推求出[η]值的方法称为“稀释法”或“外推法”。第一次测定用浓度较 大的少量溶液，然后依次将一定量的溶剂加入粘度汁中，稀释成不同浓度的溶液。这样．可 以减少洗涤粘度计的次数。

在实际工作中，由于试祥量少，或者需要测定同一品种的大量试样，为了简化实验 操作，可以在一个浓度下测定η_sp 或η_r ，直接求 [η]，而不需要作浓度外推。这种方法俗 称“一点法”。

表述溶液粘度和浓度关系的经验式很多，式中的参数 K ' 、β、K_I、n 等对给定的高 分子—溶剂体系是一常数，与分子量无关。所以，只要对每一体系定出参数数值后，就 可以从一个浓度的溶液粘度计算特性粘度。