纳米压痕能完成多种力学性能的测试，最直接测量的是硬度(H)和弹性模量(E)；对不会导致压痕周围凸起(pile-up)的材料，如大多数陶瓷、硬金属和加工硬化的软金属，硬度和弹性模量的测量精度通常优于10%。

在加载过程中，试样首先发生弹性变形，随着载荷的增加，试样开始发生塑性变形，加载曲线呈非线性；卸载曲线反映了被测物体的弹性恢复过程。通过分析加卸载曲线可以得到材料的硬度和弹性模量等。图3(a)给出了典型的整个加载和卸载过程中的压痕载荷(1oad or load onsample)P与位移(displacement or displacement into surface)h之间关系的曲线．图3(b)为一轴对称压头(tip)在加卸载过程中任一压痕剖面的示意图。在压头压入材料的过程中，材料经历了弹性和塑性变形，产生了同压头形状相一致的压痕接触深度(contact depth)h_c和接触圆半径(radius of the circle of contact)a。在压头退出过程中，仅弹性位移恢复。硬度和弹性模量可从最大压力P_max，最大压入深度h_max，卸载后的残余深度h_f和卸载曲线的端部斜率S=dP/dh(称为弹性接触刚度elastic contact stifness)中获得。

假设：试样为各向同性材料，其几何尺寸远大于压痕的尺寸；材料表面平整；不存在与时间相关的变形，即无蠕变和黏弹性。定义硬度H（hardness）和复合响应模量E_r（composite responsemodulus）

式中P为在任意压痕深度的实时载荷，A为在P作用下接触表面的投影面积。根据此定义，纳米压痕硬度是材料对接触载荷承受能力的量度。这里，请注意该定义与传统显微硬度定义(H=P_max/A_residual)的区别。对于塑性形变起主要作用的过程，两种定义给出类似的结果；但是，对于弹性形变为主的接触过程，两种定义将给出完全不同的硬度。因为纯弹性接触过程，剩余接触面积非常小，传统的定义将导致硬度无穷大。式(2)来源于弹性接触理论，可以被用来解释压头和试样的弹性形变，β为与压头形状有关的常数。对不同形状的压头，β数值不同：

圆形压头β=1.000，Berkovich(三棱锥)压头=1.034，Vickers压头(四棱锥) =1.012。被测试样的弹性模量可从下式中获得

式中E，v分别为被测材料的弹性模量和泊松比；E_i，v_i分别为压头的弹性模量和泊松比。对于金刚石压头E_i= 1141 GPa，v_i= 0.07。这里，要计算出E，必须先知道v。粗略估计一下，当v= 0.25±0.1，对大多数材料的弹性模量E仅会产生5.3%的不确定度。所以，在不知道被测材料的情况下，可取v= 0.25，这样不会引起较大的误差。

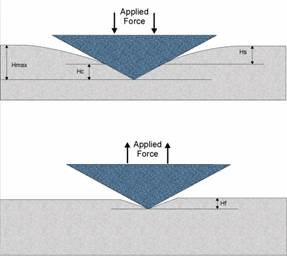
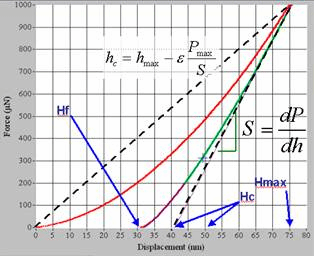
图3

为了从载荷一位移数据计算出硬度和弹性模量，必须准确地知道弹性接触刚度和接触面积。通过卸载后的残余压痕照片获得投影接触面积，很不方便，对于纳米尺度的压痕，这几乎不可能。只有通过连续载荷-位移曲线如图2(a)计算出接触面积。目前，Oliver-Pharr法是计算接触面积最常用的方法。这种方法通过如下函数拟合载荷-位移曲线的卸载部分。

式中B和m是通过测量获得的拟合参数，h_f为完全卸载后的位移。弹性接触刚度便可以根据式(4)的微分计算出

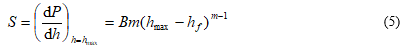
对于一条拟合的卸载曲线，式(5)不一定总能提供正确的描述。例如，对附着在基底上的薄膜材料，式(5)就不一定总是正确的。在这种情况下，根据整条卸载曲线拟合得到的参量常常导致非常大的误差。因此，确定接触刚度的曲线拟合通常只取卸载曲线顶部的25%~50%。对于弹性接触，接触深度(h_c)总是小于压入深度(即最大位移h)，由下式计算

式中ε为与压头形状有关的常数。对于球形或棱锥形(如Berkovich和Vickers)压头，ε=0.75；锥形压头，ε=0.72。虽然式(6)来源于弹性接触理论，但对塑性变形也符合得相当好。值得注意的是，式(6)不能说明凸起(pile—up)的塑性现象，因为假设接触深度总是小于压入深度。接触面积的投影A可由经验公式A=f(h_c)计算。对于一个理想的Berkovich压头，A=24.56h_c²。