取相距为dy的两薄层流体,下层静止,上层有一剪切力F,使其产生一速度du。由于流体间有内摩擦力影响,使下层流体的流速比紧贴的上一层流体的流速稍侵一些,至静止面处流体的速度为零,其流速变化呈线性。这样,在运动和静止面之间形成一速度梯度du/dy,也称之为剪切速率。
在稳态下,施于运动面上的力F,必然与流体内因勤性而产生的内摩擦力相干衡,根据牛顿黏性定律.施于运动面上的剪切应力,与速度梯度du/dy成正比。即:
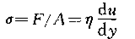 8-1
8-1
式中,du/dy为剪切速率,用γ表示;η为比例常数,称为黏度系数,简称黏度。上式可改写为:
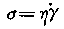 8-2
8-2
以剪切应力σ。对剪切速率γ作图,所得的图线称为剪切流动曲线,简称流动曲线。
(1)牛顿流体的流动曲线是通过坐标原点的—直线,其斜率即为黏度,即牛顿流体的剪切应力与剪切速率之间的关系完全服从于牛顿黏性定律:σ/γ=η,水、酒精、醇类、酯类、油类等均属于牛顿流体。
(2)凡是流动曲线不是直线或虽为直线但不通过坐标轴原点的流体,都称之为非牛顿流体。此时强度随剪切速率的改变而改变,这时将教度称为表现强度,用Va来表示。聚合物浓溶液、熔融体、悬浮体、浆状浓等大多属于此类。
聚合物流体多数属于非牛顿流体,它们与牛顿流体具有不同的流动特性,两者的动量传递特性也有所差别,进而影响到热量传递、质量传递及反应结果。对于某些聚合物的浓溶液通常用ostwald幂律定律来描述它的数弹性,即:
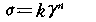 8-3
8-3
式中,n为流动幂律指数,k为稠度系数(常数)。
对比式(2—104)、(2—105),表观黏度ηa可以用kγn来表示,即
ηa=kγn。
幂律定律在表征流体的熟弹性上的优点是通过n值的大小能判定流体的性质。n>1,为胀塑性流体;n<1,为假塑性流体;n=l为牛顿流体。胀塑性流体和假塑性流体都属于非牛顿流体。可用图2—105来表示。
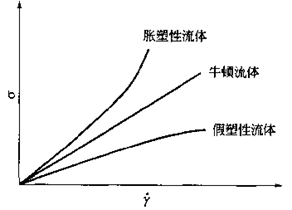
几种典型的流变曲线
将式(2—104)两边取对数得:
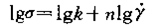
用lgσ对lgγ作图得一直线,n值及k值即可定量求出。