1.概述 材料的内应力是指当产生应力的各种因素不复存在时(如外力已经去除、温度已达均匀,相变已经停止等),由于不均匀的塑形变形或者相变而使材料内部依然存在的并自身保持平衡的应力,这种应力将导致晶格畸变。内应力分为两类:第一类是在物体较大范围内存在并保持平衡的应力,称之为宏观应力(工程上也称为残余应力),它会引起衍射峰位的偏移:当存在压应力时,晶面间距变小,衍射峰向高角度偏移,反之,当存在拉应力时,晶面间的距离被拉大, 导致衍射峰位向低角度位移。而且移动距离的大小与应力大小相关。第二类是 在一个或少数晶粒范围内或若干个原子范围内存在并保持平衡的内应力,称为微观内应力(各种晶体缺陷以及微观不均匀的变形和相变引起的应力场),一般使衍射峰变宽。
实际构件中的残余应力对其尺寸稳定性和使用寿命等有着直接的影响。通过测定构件的残余应力,可以控制车削、磨削等加工工艺,检查焊接、热处理、表面强化处理以及消除应力处理等工序的工艺效果,并可测定疲劳强度的储备 情况,分析构件的失效原因,因此,残余应力的测定具有重要的实际意义。
X射线衍射法通过测量材料的应变再按弹性定律求得残余应力。
2.原理
含有宏观残余应力的物体,在较小的体积范围内,弹性应变大体上是均匀 分布的,同时,物体的表面不存在三轴应力,假设其主应力σ1和σ2平行于 试样表面,在试样表面法线方向σ3=0,如图4-1所示。这时,垂直表面方向 的正应变是
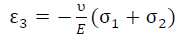 (4-1)
(4-1)

图 4-1
如图4-1,OA方向的方向余弦是cosα、cosβ、cosψ(其中α、β、ψ分别是OA方向与σ1、σ2、σ3之间所夹的空间角),则该方向的正应变是:
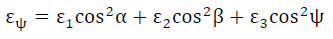 (4-2)
(4-2)
过σ3与OA做一个平面OACB,其中OB(σx方向)与σ1的夹角为蠁, 通过角度关系可以把上式改成
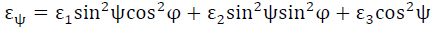 (4-3)
(4-3)
令σx和𝜀x分别是物体表面𝑥方向的残余应力及应变,则有
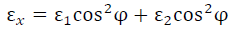 (4-4)
(4-4)
 (4-5)
(4-5)
式中υ为泊松比,E为弹性摸量
当残余应力是定值时,σx和𝜀x都是常数。εψ是蠄角的函数,把式4-5予以sin2ψ为变量求导,则
 (4-6)
(4-6)
这时的残余应力测量就成为了εψ门与sin2ψ的关系了。 没有应力时,如果用一束单色X射线对物体入射,则衍射条件满足布拉格方程:
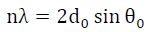 (4-7)
(4-7)
式中 n—反射极数
位—入射线的波长
d0—衍射晶面的晶面间距
θ0—入射角
物体内部如果有弹性应变,晶面间距将发生变化,就代表这组晶面的正 应变。把式4-7微分后,可得
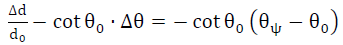 (4-8)
(4-8)
若把图中的OA方向看成衍射面的法线方向,则ψ是这一方向与试样表面 法线方向的夹角,θψ是有应力情况下的衍射角。蠄方向的线应变是:
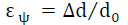 (4-9)
(4-9)
把式 4-9 和式 4-8 代入式 4-6 得
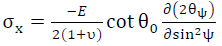 (4-10)
(4-10)
令
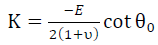 (4-11)
(4-11)
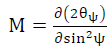 (4-12)
(4-12)
则
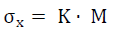 (4-13)
(4-13)
式4-11的量都是常数,不难计算出K值。而计算M值时,要以不同的几个 角度ψ把X射线投射到试样表面,利用扫描计数器测出衍射的位置2θψ,并且以2θ门对sin2ψ作图得到曲线,该曲线的斜率就是式4-12的M值了。最后, 试样表面𝑥方向的应力就能按式4-13求出。
3.实验方法
在使用衍射仪测量应力时,试样与探测器θ~2θ关系联动,属于固定ψ法。
通常ψ等于0°、15°、30°、45°测量四次。当ψ= 0时,与常规使用衍射仪的方法一样,将探测器(计数管)放在理论算出的衍射角2θ处,此时入射线及衍射线相对于样品表面法线呈对称放射配置。然后使试样与探测器按θ~2θ联动。在2θ处附近扫描得出指定的HKL衍射线的图谱。当ψ≠ 0时,将衍射仪测角台的θ~2θ联动分开。先使样品顺时针转过一个规定的ψ角后,而探测器仍处于0,然后联上θ~2θ联动装置在2θ处附近进行扫描,得出同一条HKL衍射线的图谱。
作2θ−sin2ψ的关系直线,最后按应力表达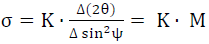 求出应力值。
求出应力值。