磁性材料应用广泛，从常用的永久磁铁、变压器铁芯到录音、录像、计算机存储用的磁带、磁盘等都采用磁性材料。磁滞回线和基本磁化曲线反映了磁性材料的主要特征。通过实验研究这些性质不仅能掌握用示波器观察磁滞回线以及基本磁化曲线的基本测绘方法，而且能从理论和实际应用上加深对材料磁特性的认识。

铁磁材料分为硬磁和软磁两大类，其根本区别在于矫顽磁力Hc的大小不同。硬磁材料的磁滞回线宽，剩磁和矫顽力大（达120-20000A/m以上），因而磁化后，其磁感应强度可长久保持，适宜做永久磁铁。软磁材料的磁滞回线窄，矫顽力Hc一般小于120A/m，但其磁导率和饱和磁感强度大，容易磁化和去磁，故广泛用于电机、电器和仪表制造等工业部门。磁化曲线和磁滞回线是铁磁材料的重要特性，也是设计电磁机构作仪表的重要依据之一。

本实验采用动态法测量磁滞回线。需要说明的是用动态法测量的磁滞回线与静态磁滞回线是不同的，动态测量时除了磁滞损耗还有涡流损耗，因此动态磁滞回线的面积要比静态磁滞回线的面积要大一些。另外涡流损耗还与交变磁场的频率有关，所以测量的电源频率不同，得到的B-H曲线是不同的，这可以在实验中清楚地从示波器上观察到。

1、磁化曲线

如果在由电流产生的磁场中放入铁磁物质，则磁场将明显增强，此时铁磁物质中的磁感应强度比单纯由电流产生的磁感应强度增大百倍，甚至在千倍以上。铁磁物质内部的磁场强度H与磁感应强度B有如下的关系：

B=μH

对于铁磁物质而言，磁导率μ并非常数，而是随H的变化而改变的物理量，即μ=ƒ（H），为非线性函数。所以如图2-1所示，B与H也是非线性关系。 

铁磁材料的磁化过程为：其未被磁化时的状态称为去磁状态，这时若在铁磁材料上加一个由小到大的磁化场，则铁磁材料内部的磁场强度H与磁感应强度B也随之变大，其B-H变化曲线如图2-1所示。但当H增加到一定值（Hs）后，B几乎不再随H的增加而增加，说明磁化已达饱和，从未磁化到饱和磁化的这段磁化曲线称为材料的起始磁化曲线。如图2-1中的OS端曲线所示。

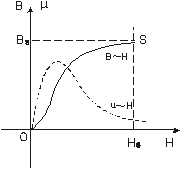
图2-1磁化曲线和μ～H曲线图

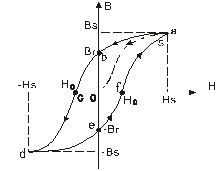
图2-2起始磁化曲线与磁滞回线

2、磁滞回线

当铁磁材料的磁化达到饱和之后，B几乎不再随H的增加而增加，此时B=Bs称为饱和磁感应强度。如果将磁化场减少，则铁磁材料内部的B和H也随之减少，但其减少的过程并不沿着磁化时的OS段退回。从图2-2可知当磁化场撤消，H=0时，磁感应强度仍然保持一定数值B=Br称为剩磁（剩余磁感应强度）。

若要使被磁化的铁磁材料的磁感应强度B减少到0，必须加上一个反向磁场并逐步增大。当铁磁材料内部反向磁场强度增加到H=Hc时（图2-2上的c点），磁感应强度B才是0，达到退磁。图2-2中的的bc段曲线为退磁曲线，Hc为矫顽磁力。如图2-2所示，当H按O→Hs→O→Hc→Hs→O→Hc→Hs→的顺序变化时，B相应沿O→Bs→O→Br→O→Bs→Br→O→Bs顺序变化。图中的Oa段曲线称起始磁化曲线，所形成的封闭曲线abcdefa称为磁滞回线。bc曲线段称为退磁曲线。由图2-2可知：

（1）当H=0时，B≠0，这说明铁磁材料还残留一定值的磁感应强度Br，通常称Br为铁磁物质的剩余感应强度（剩磁）。

（2）若要使铁磁物质完全退磁，即B=0，必须加一个反方向磁场Hc。这个反向磁场强度Hc，称为该铁磁材料的矫顽磁力。

（3）B的变化始终落后于H的变化，这种现象称为磁滞现象。

（4）H上升与下降到同一数值时，铁磁材料内的B值并不相同，退磁化过程与铁磁材料过去的磁化经历有关。

（5）当从初始状态H=0，B=0开始周期性地改变磁场强度的幅值时，在磁场由弱到强地单调增加过程中，可以得到面积由大到小的一簇磁滞回线，如图2-3所示。其中最大面积的磁滞回线称为极限磁滞回线。

（6）由于铁磁材料磁化过程的不可逆性及具有剩磁的特点，在测定磁化曲线和磁滞回线时，首先必须将铁磁材料预先退磁，以保证外加磁场H=0，B=0；其次，磁化电流在实验过程中只允许单调增加或减少，不能时增时减。在理论上，要消除剩磁Br，只需通一反向磁化电流，使外加磁场正好等于铁磁材料的矫顽磁力即可。实际上，矫顽磁力的大小通常并不知道，因而无法确定退磁电流的大小。我们从磁滞回线得到启示，如果使铁磁材料磁化达到磁饱和，然后不断改变磁化电流的方向，与此同时逐渐减少磁化电流，直到等于零。则该材料的磁化过程中就是一连串逐渐缩小而最终趋于原点的环状曲线，如图2-4所示。当H减小到零时，B亦同时降为零，达到完全退磁。

实验表明，经过多次反复磁化后，B-H的量值关系形成一个稳定的闭合的“磁滞回线”。通常以这条曲线来表示该材料的磁化性质。这种反复磁化的过程称为“磁锻炼”。本实验使用交变电流，所以每个状态都是经过充分的“磁锻炼”，随时可以获得磁滞回线。

我们把图2-3中原点O和各个磁滞回线的顶点a₁,a₂，…a所连成的曲线，称为铁磁性材料的基本磁化曲线。不同的铁磁材料其基本磁化曲线是不相同的。为了使样品的磁特性可以重复出现，也就是指所测得的基本磁化曲线都是由原始状态（H=0，B=0）开始，在测量前必须进行退磁，以消除样品中的剩余磁性。

在测量基本磁化曲线时，每个磁化状态都要经过充分的“磁锻炼”。否则，得到的B-H曲线即为开始介绍的起始磁化曲线，两者不可混淆。

3、示波器显示B—H曲线的原理线路

示波器测量B—H曲线的实验线路如图2-5所示。

本实验研究的铁磁物质是一个环状试样（如图2-6所示）。在试样上绕有励磁线圈N₁匝和测量线圈N₂匝。若在线圈N₁中通过磁化电流i₁时，此电流在试样内产生磁场，根据安培环路定律HL=N₁i₁，磁场强度H的大小为：

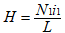        （2-1）

其中L为的环状试样的平均磁路长度。（在图1-2-6中用虚线表示）。

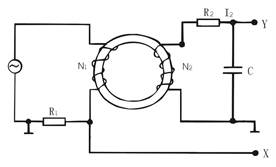
图2-5示波器测量B—H曲线的实验线路

 图2-6环状式样

由图2-5可知示波器X轴偏转板输入电压为：

U_x=U_R=i₁R₁         （2-2）

由式（2-1）和式（2-2）得：

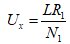         （2-3）

上式表明在交变磁场下，任一时刻电子束在X轴的偏转正比于磁场强度H。

为了测量磁感应强度B，在次级线圈N₂上串联一个电阻R₂与电容C构成一个回路，同时R₂与C又构成一个积分电路。取电容C两端电压Uc至示波器Y轴输入，若适当选择R₂和C使R₂〉〉1/ωC，则：

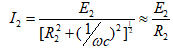
式中，ω为电源的角频率，E₂为次级线圈的感应电动势。

因交变的磁场H的样品中产生交变的磁感应强度B，则：

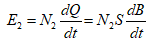
式中S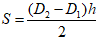（）为环试样的截面积，设磁环厚度为h则：

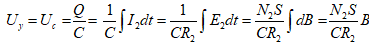（1-2-4）

上式表明接在示波器Y轴输入的U_y正比于B。

R₂C构成的电路在电子技术中称为积分电路，表示输出的电压Uc是感应电动势E₂对时间的积分。为了如实地绘出磁滞回线，要求：

（1）

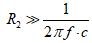
（2）在满足上述条件下，Uc振幅很小，不能直接绘出大小适合需要的磁滞回线。为此，需将Uc经过示波器Y轴放大器增幅后输至Y轴偏转板上。在较低的频率时，磁滞回线经常会出现如图2-7所示的畸变。这时需要选择合适的R₁、R₂和C的阻值，可避免这种畸变，得到最佳磁滞回线图形。这样，在磁化电流变化的一个周期内，电子束的径迹描出一条完整的磁滞回线。适当调节示波器X和Y轴增益，再由小到大调节信号发生器的输出电压，即能在屏上观察到由小到大扩展的磁滞回线图形。逐次记录其正顶点的坐标，并在坐标纸上把它联成光滑的曲线，就得到样品的基本磁化曲线。

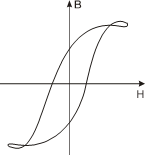
图2-7磁滞回线的畸变

4、示波器的定标

从前面说明中可知从示波器上可以显示出待测材料的动态磁滞回线，但为了定量研究磁化曲线磁滞回线，必须对示波器进行定标。即还须确定示波器的X轴的每格代表多少H值（A/m），Y轴每格实际代表多少B（T）。（见参考文献1的P143）

由公式（2-3）、（2-4）可以得知，在U_x、U_y可以准确测得且R₁、R₂和C都为已知的标准元件的情况下，就可以省去繁琐的定标工作（见参考文献1的P143～144）。下面就如何在这种情况下测量进行分析。

一般示波器都有已知的X轴和Y轴的灵敏度，设X轴灵敏度为S_x（V/格），Y轴的灵敏度为S_y（V/格）。将X轴、Y轴的灵敏度旋钮顺时针打到底并锁定，则上述S_x和S_y均可从示波器的面板上直接读出，则有：

U_x=S_xX，U_y=S_yY

式中X，Y分别为测量时记录的坐标值（单位：格。注意，指一大格,，示波器一般有8~10大格），可见通过示波器就可测得U_x、U_y值。

由于本实验使用的R₁、R₂和C都是阻抗值已知的标准元件，误差很小，其中的R₁R₂为无感交流电阻，C的介质损耗非常小。这样就可结合示波器测量出H值和B值的大小。

综合上述分析，本实验定量计算公式为：

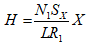        （2-5）

        （2-6）

式中各量的单位为：R₁，R₂为Ω；L为m；S为m²；C为F；S_x，S_y为V/格；X，Y为格（分正负向读数）；H的单位为A/m；B的单位为T。